こんにちはSGKです。

今回も惑星の軌道計算から一般相対性理論をプログラムに起こすため頑張ります。

で、「アインシュタインに挑戦」とか意気込んでみたがその前に挑戦しなければいけない方がいます。
それはニュートンさんです。

ニュートンは「リンゴが落ちた」とか言って万有引力を発見した事は知っていましたが、微分積分の秘密を解いて惑星の軌道計算をしたスゲー人です。
300年ぐらい前の人で日本はその時江戸時代初期！

天文学では、おはようガリレオ、こんにちはニュートン、おやすみなさいアインシュタインな感じの人っぽい。

ちなみに「リンゴが落ちた」で発見したのは「万有引力」であって「重力」ではない。
落ちたリンゴを見て「リンゴも地球を引っ張っているのでは？」という発想のようで、そこからして「太陽が地球を、地球が太陽を、地球が月を、月が地球を」とか思いめぐって軌道計算とかやっちゃうんだろうな、スゲー人です。

なので今回は微分について書きたいと思います。

微分とは？

微分とは一文で説明すると、「ある関数のある点における瞬間の変化率、接線の傾きを求めるための関数を求めること」だそうです。

「ある関数」とか言われるとわかりにくいですが、「y = x²」のような式を関数と称し、 x に任意の値を代入して計算した結果をグラフに置き換えると分かりやすいです。

「ある点における瞬間」とは x に代入した値がその瞬間、と考えると分かりやすいでしょうか？
グラフで表せば赤い点を置いた位置がその瞬間とすると x が 2 の瞬間 y は 4 です。

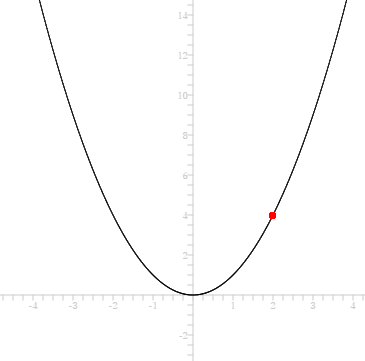
その x が 2 のときの接線の傾きを求めるためにはどうするか、という式を求めるのが微分です。

接線

接線とは曲線に対して、その曲線上の1点で接する直線の事です。
例えば x が 2 の瞬間の傾きを求めるためには以下のグラフのように曲線に2点が交わる直線の一方の点をもう一方に近づけて直線を引くと、その線は接線に近づいていくため、「2点の間が限りなく 0 に近づいたときの線はもう接線だよね？」という事をニュートンは発見しました。

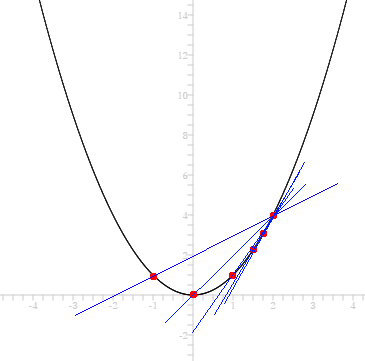
この2点の間が限りなく 0 に近い線の傾きを導き出すものを式にすると「y’ = 2x」となります。

※この辺は説明が足りないですが細かく説明するには難しいし長くなるので詳しくは後記の出展をご拝読下さい、、

たとえばこの「y’ = 2x」の関数の x が 2 の場合は「y’ = 2 × 2」で、傾き y’ は 4 です。
これは x が 1 増えるとに y が 4 増えるような傾きの直線を示しており、これが「y = x²」の x が 2 の場合の接線です。

この接線を求めることができる関数「y’ = 2x」を導関数と称し、「y = x²」から「y’ = 2x」を求めることを微分といいます。
微分には公式があり、それが「y’ = nx^n-1」です。 高校生の時に覚えたかもしれないヤツです。

※ちなみに微分した後の「y」が「y’」（ワイダッシュ）になっているのは元の「y = x²」の「y」とは違う値になる事を意味しています。

この公式はより複雑な「y = 2x³ – 4x² + 5x + 7」のような式にも適用可能で、これを微分した導関数は「y’ = 6x² – 8x + 5」となります。

微分で何がわかる？

微分・導関数で何がわかるのかというと、その瞬間の（式でいえば「x」の位置での）力の方向とか変化の様子がわかるようです。
と言われてもなので、１つ簡単な例を示したいと思います。

例えば以下のグラフのような「y = x² – 5x + 8」の式で描かれた軌道で腕を振ってアンダースローでボールを投げる場合、

どの位置で手からボールを離せばボールが水平に真っすぐ（x 軸と並行）に飛ぶか？
（重力の影響は無いものとする）という問題があった場合、

まず微分して導関数を求めます。

y = x² – 5x + 8
↓
y’ = 2x – 5

次に x 軸と並行な接線の傾きは 0 ：「x がいくつでも y が 0 の傾き」なので、y’ に 0 を代入し計算します。

0 = 2x – 5
↓
x = 5 ÷ 2
↓
x = 2.5

という事で x が 2.5 のときに接線の傾きが 0 となり、このときにボールから手を離せばボールが水平に真っすぐ飛ぶことが分かります。

なんかこの x が 2.5 の位置をグラフで見ると y が１番小さい下の方になる位置で、こんな所で手を離したらたら早速地面に当たりそうですが、実はこの位置で離せば水平に真っすぐ飛ぶんですね！

しかし、これだけでは微分がどうやって惑星の軌道計算につながるか分かりません。。
さらなる応用は次回の積分の回に記したいと思います。

後書

▼出展・参考はこちら、皆大好き、ニュートン大好きニュートンプレスの
ニュートンの大発明 微分と積分―これならわかる (ニュートンムック Newton別冊サイエンステキストシリーズ)｜本｜Amazon
なのですが、もう販売していないようなので、現行版と思われる

▼以下でも同じような内容だと思います。
別冊 微分と積分 改訂第3版 (ニュートン別冊) |本 | 通販 | Amazon
ときどき読みますが、天文・数学・医学など幅広くサイエンスを扱う「Newton」って月刊誌を出しているだけあって、この本を読んで改めて気づかされた！ニュートン愛にあふれる出版社ですね！

▼加えてグラフの画像はこちらのサイトで描画したものを利用させてもらいました。
ガスコン研究所 (gascon.jp)
いずれこのサイトの JavaScript コードを参考にさせてもらって何か動くものも作りたい、、

シリーズ

• アインシュタインに挑戦：プロローグ
• その１-微分